√ (a+b)^3 formula expansion 130628-How to expand a^3-b^3

=SUM(*$E$29,C3*$E$30,D3*$E$31) by the way you can have the short cut by clicking the E29 in the formula bar and press F4 on your keyboard it will result like above formula The meaning of the $ dollar sign in the cell address is to make it fix and constant(abcde) 3 a 3 b 3 c 3 d 3 e 3 As usual, the cubics have a coefficient 1 There are 5 different letters, so we have 5 cubics The sum of the coefficients is 1·5=5 3a²b3a²c3a²d3a²e 3b²a3b²c3b²d3b²e 3c²a3c²b3c²d3a²e 3d²a3d²b3d²c3d²e 3e²a3e²b3e²c3e²d= 3*2*1 = 6, 2!

Expand Using Identity 2x 3y 3

How to expand a^3-b^3

How to expand a^3-b^3-In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial According to the theorem, it is possible to expand the polynomial n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive integer depending on n and b For example, 4 = x 4 4 x 3 y 6 x 2 y 2 4 x y 3 y 4 {\displaystyle ^{4}=x^{4}4x^{3}y6x^{2}y^{2}4xy^{3}y^{4}} TheLet the literals a and b represent two terms in algebraic form The subtraction of b from a is written as a − b It is basically an algebraic expression and also a binomial The square of this expression is written as ( a − b) 2 in mathematical form and it is expanded as a 2 − 2 a b b 2 mathematically In mathematics, this algebraic identity is used as a formula and it is called in the following three ways

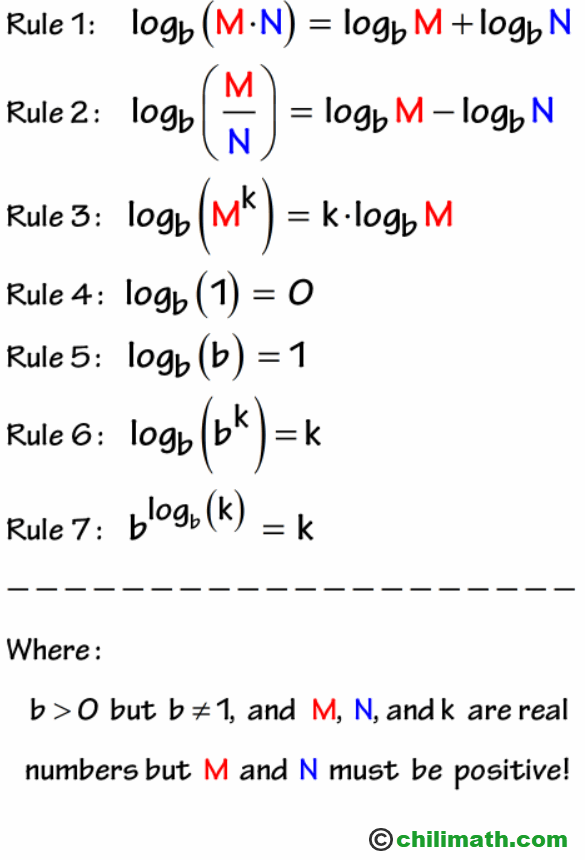
Logarithm Rules Chilimath

(a b) 3 = a 3 b 3 3ab(a b) (a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 = a 3 – b 3 – 3ab(a – b) a 3 – b 3 = (a – b)(a 2 ab b 2 )A^3 3a^2b 3ab^2 b^3 Use the Binomial expansion (note the exponents sum to the power in each term) (xy)^3 = _3C_0x^3y^0 _3C_1x^2y^1 _3C_2x^1y^2 _3C_3x^0y^3 Remember 3!A1/3 a1/3 a1/3 = a (24) (a1/3)3 = a (25) (a2)1/3 = (a1/3)2 = a2∕3 (26) (a1/3)1/4 = a1/3 1/4 = (a1/4)1/3 (27) (a b)1/3 = a1/3 b1/3 (28) (a / b)1/3 = a1/3 / b1/3 (29) (1 / a)1/3 = 1 / a1/3 = a1/3 (30) Sponsored Links Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and more

That is, for each term in the expansion, the exponents of the x i must add up to n Also, as with the binomial theorem, quantities of the form x 0 that appear are taken to equal 1 (even when x equals zero) In the case m = 2, this statement reduces to that of the binomial theorem Example The third power of the trinomial a b c is given by= 1 and 0!(a b) 2 = (a b)(a b) = a 2 2ab b 2 (a − b) 2 = (a − b)(a − b) = a 2 − 2ab b 2 Example 3 Expand the given expression, clicking on the equal signs to see the next step (

A 3 – b 3 = (a – b) (a 2 ab b 2) a 3 b 3 = (a b) (a 2 – ab b 2) (a b) 3 = a 3 3a 2 b 3ab 2 b 3 (a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 (a b – c) 2 = a 2 b 2 c 2 2ab – 2bc – 2ca (a – b c) 2 = a 2 b 2 c 2 – 2ab – 2bc 2ca (a – b – c) 2 = a 2 b 2 c 2 – 2ab 2bc – 2ca (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2caPipes Heat Expansion and Cooling Contraction Expansion or contraction when heating or cooling cast iron, carbon and carbon molybdenum steel, wrought iron, copper, brass and aluminum pipes Pipes and Tubes Temperature Expansion Pipes expands when heated and contracts when cooled and the expansion can be expressed with the expansion formulaEuler's formula then comes about by extending the power series for the exponential function to the case of x= i to get exp(i ) = 1 i 2 2!

What Is The Formula Of Math A 3 B 3 Math Quora

Binomial Expansion Using A General Formula Quick Visual Summary With Space For Students To Really Embed T Binomial Theorem This Or That Questions The Expanse

Binomial Theorem The Expansion of (a b)n If n is any positive integer, then ( a b) n = a n n C 1 a n − 1 b n C 2 a n − 2 b 2 ⋯ n C m a n − m b m ⋯ b n Where n C m = combination of n objects taken m at a time Some Example of Binomial Expansion ( a b) 2 = a 2 2 a b b 2 ( a b) 3 = a 3 3 a 2 b 3 a b 2 b 3Solution We have (a b) n, where a = 2/x, b = 3√ x, and n = 4 Then using the binomial theorem, we have Then using the binomial theorem, we have Finally (2/x 3√ x ) 4 = 16/x 4 96/x 5/2 216/x 216x 1/2 81x 2A³ b³ = (a b)(a² – ab b²)

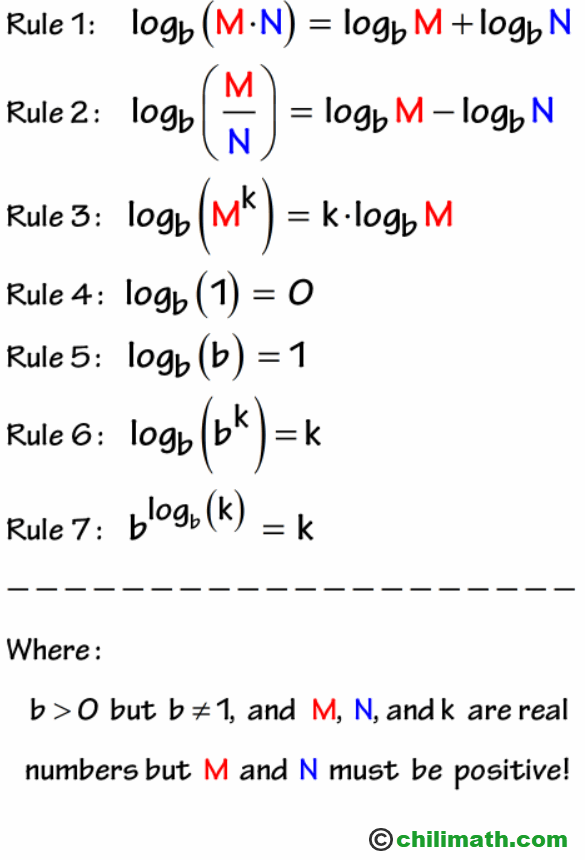
Logarithm Rules Chilimath

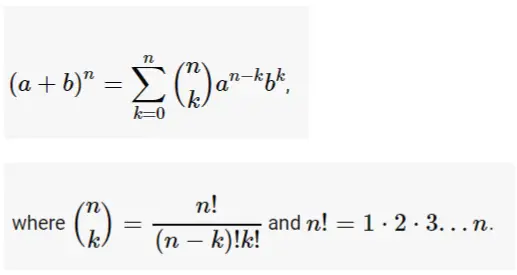
Binomial Expansion Calculator Free Tool To Expand Using Binomial Theorem Onlinecalculator Guru

Binomial theorem, statement that for any positive integer n, the nth power of the sum of two numbers a and b may be expressed as the sum of n 1 terms of the form in the sequence of terms, the index r takes on the successive values 0, 1, 2,, n The coefficients, called the binomial coefficients, are defined by the formula(a b) 3 = a 3 b 3 3ab(a b) (a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 = a 3 – b 3 – 3ab(a – b) a 3 – b 3 = (a – b)(a 2 ab b 2 )Expansions Which Have LogarithmBased Equivalents Summantion Expansion Equivalent Value Comments x n

Algebra Formula Definition Formulas And Examples

Expanding Algebraic Expressions Using Identities Worksheets

In algebra, a quadratic equation (from the Latin quadratus for "square") is any equation that can be rearranged in standard form as = where x represents an unknown, and a, b, and c represent known numbers, where a ≠ 0If a = 0, then the equation is linear, not quadratic, as there is no term The numbers a, b, and c are the coefficients of the equation and may be distinguished by callingOne way to Do this, is to first learn what is (A B) ^3 by just multiplying A B with itself 3 times and you will have (A B)^3 = A^3 3A^2B 3AB^2 B^3 Now replace A by a and B by (b c) and Do the Work !In mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomials The expansion is given by ( a b c ) n = ∑ i j k = n i , j , k ( n i , j , k ) a i b j c k , {\displaystyle (abc)^ {n}=\sum _ {\stackrel {i,j,k} {ijk=n}} {n \choose i,j,k}\,a^ {i}\,b^ {\;\!j}\;\!c^ {k},}

What Is The Formula Of Math A 3 B 3 Math Quora

4 The Binomial Theorem

(a b) 3 = a 3 3a 2 b 3ab 2 b 3;In mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomials The expansion is given by ( a b c ) n = ∑ i j k = n i , j , k ( n i , j , k ) a i b j c k , {\displaystyle (abc)^ {n}=\sum _ {\stackrel {i,j,k} {ijk=n}} {n \choose i,j,k}\,a^ {i}\,b^ {\;\!j}\;\!c^ {k},}Let the literals a and b represent two terms in algebraic form The subtraction of b from a is written as a − b It is basically an algebraic expression and also a binomial The square of this expression is written as ( a − b) 2 in mathematical form and it is expanded as a 2 − 2 a b b 2 mathematically In mathematics, this algebraic identity is used as a formula and it is called in the following three ways

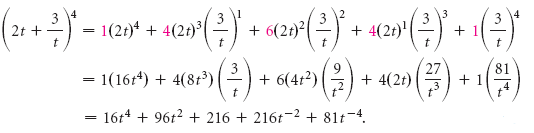
The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets

11 10 The Binomial Formula Recall A B 2 A 2 2ab B 2 For Any Binomial Expansion A B N There Are N 1 Terms Each Term Is N Th Degree Ppt Download

$$(a b c)^3 = (a^3 b^3 c^3) (3a^2b 3a^2c 3abc) (3ab^2 3b^2c 3abc) (3ac^2 3bc^2 3abc) 3abc$$ $$(a b c)^3 = (a^3 b^3 c^3) 3a(ab ac bc) 3b(ab bc ac) 3c(ac bc ab) 3abc$$The expansion follows the rule (ab)n = c0anb0 c1an−1b1 cn−1a1bn−1 cna0bn ( a b) n = c 0 a n b 0 c 1 a n 1 b 1 c n 1 a 1 b n 1 c n a 0 b n The values of the coefficients, from the triangle, are 1−6− 15−−15−6− 1 1 6 15 15 6 1Http//wwwfreemathvideoscom In this video playlist I will show you the basics for polynomial functions We will start with factoring polynomial equations

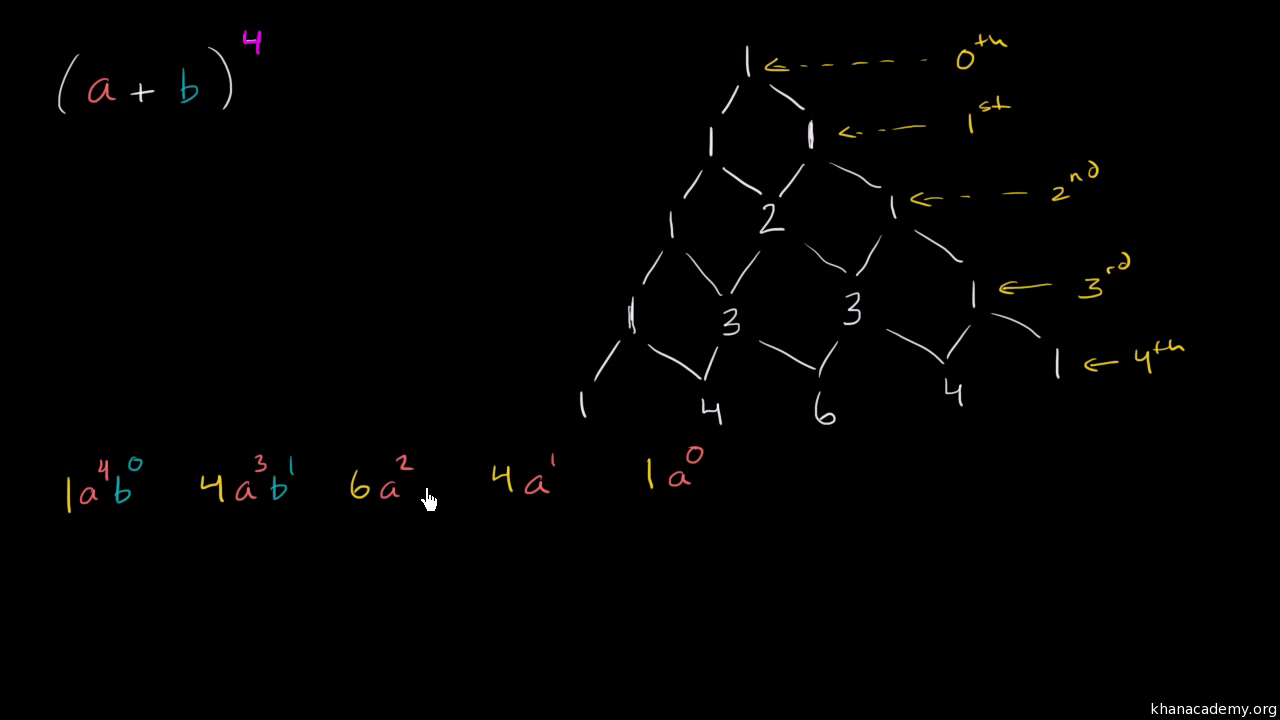
Pascal S Triangle And Binomial Expansion Video Khan Academy

What Is A B 3 Quora

And sin = 3 3!(a b)^3 = (a b) (a b) (a b) = (a*a b*a a*b b*b) (a b) = (a^2 ab ab b^2) (a b)And seeing that this is identical to the power

Solution Use The Binomial Theorem To Expand The Binomial And Express The Result In Simplified Form X 4 3

Expand Using Identity 2x 3y 3

Explanation The binomial formula that you need here is (a b)3 = a3 3a2b 3ab2 b3 Let me colour the same formula to add clarity (a b)3 = a3 3a2b 3ab2 b3 In your case, you would like to expand (2x 3)3, so your a = 2x and b = 3Answer a³ 3a²b 3ab² b³ Show more Rameshwar Lv 7 1 decade ago ( ab)^3 = ( a b)^2 (ab) = ( a^2 2ab b^2) ( a b ) = a^3 3a^2b 3b^2a b^3 = a^3 3ab ( a b) b^3 ans inIn mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomials The expansion is given by ( a b c ) n = ∑ i j k = n i , j , k ( n i , j , k ) a i b j c k , {\displaystyle (abc)^ {n}=\sum _ {\stackrel {i,j,k} {ijk=n}} {n \choose i,j,k}\,a^ {i}\,b^ {\;\!j}\;\!c^ {k},}

Binomial Theorem Wikipedia

What Is The Expansion Of A B C 3 Quora

Expansion The cube of difference between any two terms is expanded as the subtraction of three times the product of both terms and the subtraction of the second term from the first term, from the subtraction of the cube of the second term from the cube of the first term $\implies$ $(ab)^3$ $\,=\,$ $a^3b^33ab(ab)$ SimplificationThe binomial theorem states a formula for expressing the powers of sums then there is a middle term in the expansion in which the exponents of a and b are the same Only in (a) and (d), there are terms in which the exponents of the factors are the same \right)\left(\frac{a^{3} }{b^{3} } \right)\left(\frac{b^{3} }{a^{3} } \right22K views · Answer requested by

Search Q A B 5e4 Tbm Isch

Binomial Theorem Examples Solutions Examples Videos Worksheets Activities

Expansions Which Have LogarithmBased Equivalents Summantion Expansion Equivalent Value Comments x nThere are similar power series expansions for the sine and cosine, given by cos = 1 2 2!(a b) 3 = a 3 3a 2 b 3ab 2 b 3;

What Is The Formula Of Math A B 3 Math Quora

Expand And Simplify Binomial Squares 2x 3y 2 Youtube

Here a = 3x, b = 2y and c = z 3x (2y) (z) 2 = (3x) 2 (2y) 2 (z) 2 2 (3x) (2y) 2 (2y) (z) 2 (z) (3x) = 9x 2 4y 2 z 2 – 12xy 4yz – 6zx 2 Simplify a b c = 25 and ab bc ca = 59 Find the value of a 2 b 2 c 2 Solution According to the question, a b c = 25Basically you need to think of it as (ab) (ab) (ab) because that's what exponents do And then you multiply one of the (ab) parts with another (ab) Repeat with the last (ab) The webpage hasThe expansion follows the rule (ab)n = c0anb0 c1an−1b1 cn−1a1bn−1 cna0bn ( a b) n = c 0 a n b 0 c 1 a n 1 b 1 c n 1 a 1 b n 1 c n a 0 b n The values of the coefficients, from the triangle, are 1−6− 15−−15−6− 1 1 6 15 15 6 1

A B 3 Expansion Formula

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

Write the formula / expansion for (a b)3 (a b) 3 = a 3 3a 2 b 3ab 2 b 3 Substitute x for a and 2 for b (x 2) 3 = x 3 3 (x 2 ) (2) 3 (x) (2 2) 2 3 (x 2) 3 = x 3 6x 2 3 (x) (4) 8 (x 2) 3 = x 3 6x 2 12x 8 So, the expansion of (x 2)3 is x 3 6x 2 12x 8 Problem 2In using the binomial formula, we let `a = 2x,` `b = 3` and `n = 4` Substituting in the binomial formula, we get `(2x3)^4` `=(2x)^44(2x)^3(3)` `(4(3))/(2!)(2x)^2(3)^2` `(4(3)(2))/(3!)(2x)(3)^3(3)^4` `=16x^496x^3216x^2216x81`Solution We have (a b) n, where a = 2/x, b = 3√ x, and n = 4 Then using the binomial theorem, we have Then using the binomial theorem, we have Finally (2/x 3√ x ) 4 = 16/x 4 96/x 5/2 216/x 216x 1/2 81x 2

What Is The Formula For Math A 3 B 3 Math Quora

A Level Maths Binomial Expansion The Student Room

The formula is (ab)³=a³3a²b3ab²b³ You convert it to (ab)³=a³3ab(ab)b³ for an illustration You take the drawing of the formula (ab)³=a³3a²b3ab²b³ from above and replace a by the difference abWrite the formula / expansion for (a b)3 (a b) 3 = a 3 3a 2 b 3ab 2 b 3 Substitute x for a and 1 for b (x 1) 3 = x 3 3 (x 2 ) (1) 3 (x) (1 2) 1 3 (x 1) 3 = x 3 3x 2 3 (x) (1) 1 (x 1) 3 = x 3 3x 2 3x 1 So, the expansion of (x 1)3 is x 3 3x 2 3x 1To find the value of ab, we can use the formula or expansion for (a b)3 Write the formula / expansion for (a b)3 (a b) 3 = a 3 3a 2 b 3ab 2 b 3

Http Mathsathawthorn Pbworks Com F The Binomial Expansion Pdf

Algebraic Identities Standard Algebraic Identities Definition Examples

A 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abcThis applet shows the formula for sin(AB) and cos(AB) How to use the applet Change angles A and B by pressing "" and "" buttons The lengths of three arrows appear by checking "Character" box You will understand the green arrow is the sum of the red arrow and the blue arrow That indicates the formula for sin(AB)Explanation Binomial formula for (a b)3 ⇒3 C0a3b0 3 C1a2b1 3 C2a1b2 3 C3a0b3 Here, a = x and b = 1 ⇒3 C0x3 3 C1x2 × 11 3 C2x1 ×12 3 C3 × 13 As →3 C0 =3 C3 = 1 and →3 C1 =3 C2 = 3 ⇒ x3 3x2 3x 1

Expansion Archives Sat Prep

I Am Taking A Taylor Series Expansion Of A Function F X I Wish To Expand The Function Around The Value G X Is This Allowable

To find an expansion for (a b) 8, we complete two more rows of Pascal's triangle Thus the expansion of is (a b) 8 = a 8 8a 7 b 28a 6 b 2 56a 5 b 3 70a 4 b 4 56a 3 b 5 28a 2 b 6 8ab 7 b 8 We can generalize our results as follows The Binomial Theorem Using Pascal's Triangle For any binomial a b and any natural numberLet us multiply ab by itself using Polynomial Multiplication (ab) (ab) = a2 2ab b2 Now take that result and multiply by ab again (a 2 2ab b 2 ) (ab) = a3 3a2b 3ab2 b3 And again (a 3 3a 2 b 3ab 2 b 3 ) (ab) = a4 4a3b 6a2b2 4ab3 b41 decade ago We can do this if you know the Binomial Theorem But if you don't know what it is or how to use it you can do the expansion on your own (ab)^3 = (ab) (ab) (ab) This becomes (ab) (ab)^2 = (ab) (a^2 2ab b^2) = a^3 2 (a^2)b ab^2 (a^2)b 2ab^2 b^3 = a^3 3 (a^2)b 3a (b^2) b^3

Binomial Expansion Factorial Notation And Pascal S Triangle Studywell

Mast Queensu Ca Mikeroth Oldteaching Math326 Hmwk Hmwk09 Pdf

= 2*1 = 2, 1!Expansion The cube of difference between any two terms is expanded as the subtraction of three times the product of both terms and the subtraction of the second term from the first term, from the subtraction of the cube of the second term from the cube of the first term $\implies$ $(ab)^3$ $\,=\,$ $a^3b^33ab(ab)$ SimplificationProof Formula \((abc)^3 = \\a^3 b^3 c^3 6abc \\ 3ab (ab) 3ac (ac) 3bc (bc) \) Summary (abc)^3 If you have any issues in the (abc)^3 formulas, please let me know through social media and mail

What Is The Correct Formula Of Math A B 3 Math Quora

A B 3 Expansion Formula

= 1 _3C_0 = (3!)/((30)!(0!)) = (3!)/((3)!1) = 1 _3C_1 = (3!)/((31)!(1!)) = (3!)/((2)!1) = (3*2!)/(2!) = 3 _3C_2 = (3!)/((32)!(2!)) = (3!)/((1)!2!) = (3*2!)/(2!) = 3 _3C_3 = (3!)/((33)!(3!)) = (3!)/(0!*3!) = 1 Note (ab)^3 = (a (b))^3 Substitute into the BinomialA1/3 a1/3 a1/3 = a (24) (a1/3)3 = a (25) (a2)1/3 = (a1/3)2 = a2∕3 (26) (a1/3)1/4 = a1/3 1/4 = (a1/4)1/3 (27) (a b)1/3 = a1/3 b1/3 (28) (a / b)1/3 = a1/3 / b1/3 (29) (1 / a)1/3 = 1 / a1/3 = a1/3 (30) Sponsored Links Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and more

Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf

What Is The Expansion Of A B C 3 Quora

How To Expand A3 Brainly In

How To Cube Binomials

Solved Please Answer A B And C Formula 7 Is X Chegg Com

A B C 3 Formula Expansion

Math Help Algebra Quick Algebra Formulae Technical Tutoring

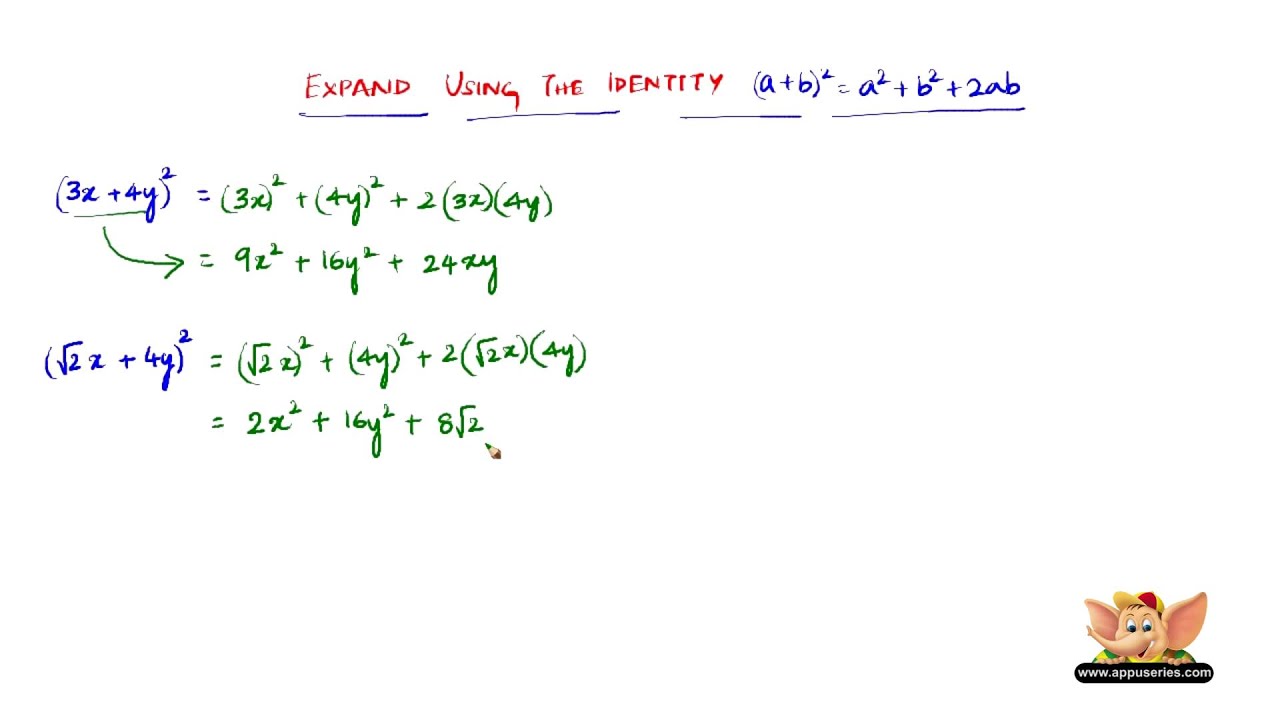
How To Expand Using The Identity A B 2 B2 2ab Youtube

Expanding Algebraic Expressions Using Identities Worksheets

Expanding Algebraic Expressions Using Identities Worksheets

Binomial Forms Expansion Of Binomial Expressions Ppt Download

A B N And A B N Formula Expander

Msbshse Solutions For Class 8 Maths Part 1 Chapter 5 Expansion Formulae Download For Free

Factorials To Binomial Theorem

Solved 2 We Ve Studied The Binomial Theorem In Class In Chegg Com

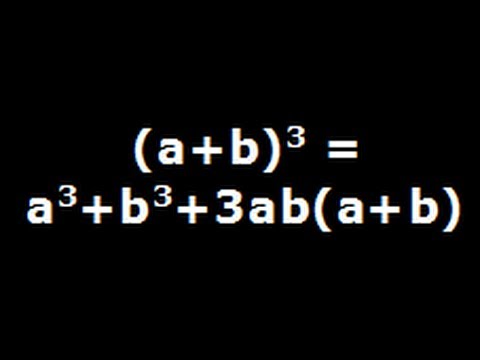
A Plus B Cube Algebra Identity Explained Step By Step Youtube

Binomial Theorem

Q Tbn And9gcrswdldblxmiitn Ggstx6knbcgxw3sex0r673zeswoh Igfkvn Usqp Cau

A B Formula Identity

Binomial Theorem Wikipedia

3 Ways To Use The Perfect Square Identity As A Shortcut In Expansion

Yismxplusc Geometric Proof Of The Cubic Formula A B 3

Intro To The Binomial Theorem Video Khan Academy

Expand And Simplify Trinomial Square A B C 2 A 2 B 2 C 2 2ab 2ac 2bc Youtube

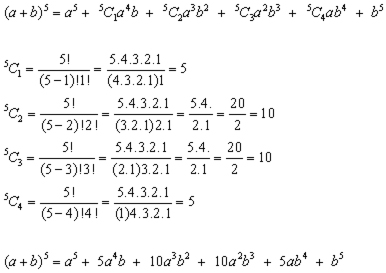
The Binomial Theorem Algebra Pure Mathematics From A Level Maths Tutor

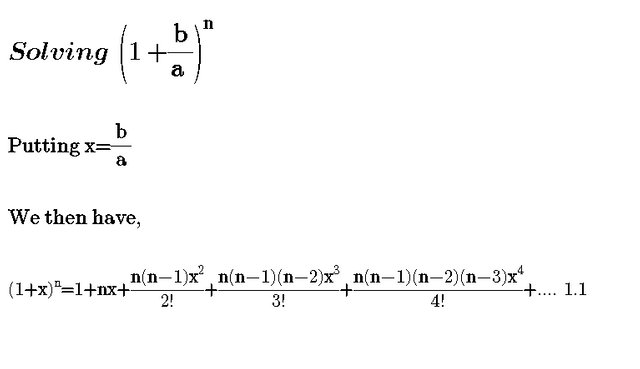
Deriving Of Binomial Expansion Formula For Two Variables A B N Steemit

The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium

2

What Is The Formula Of Math A B 3 Math Quora

3 Binomial Theorem Ghci Grade 12 Mathematics Of Data Management

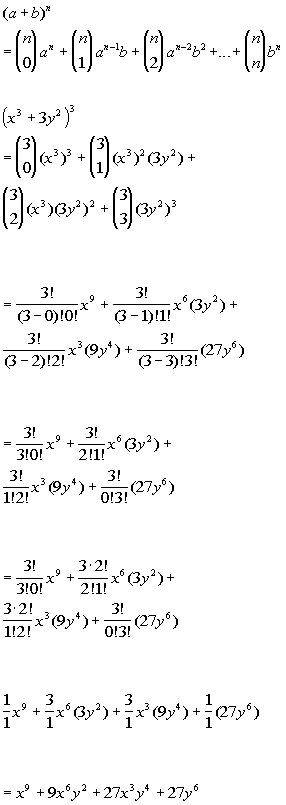
Wtamu Math Tutorials And Help

General And Middle Term Binomial Theorem Formula Videos Examples

3 Ways To Use The Perfect Square Identity As A Shortcut In Expansion

A B C 3 Formula Expansion

Expanding Algebraic Expressions Using Identities Worksheets

Solved 5 Show The Expansion And Evaluate 5 A 3 S 3 K Chegg Com

How To Develop A Numerical Differentiation Formula Using Taylor Expansion Series Mathematics Stack Exchange

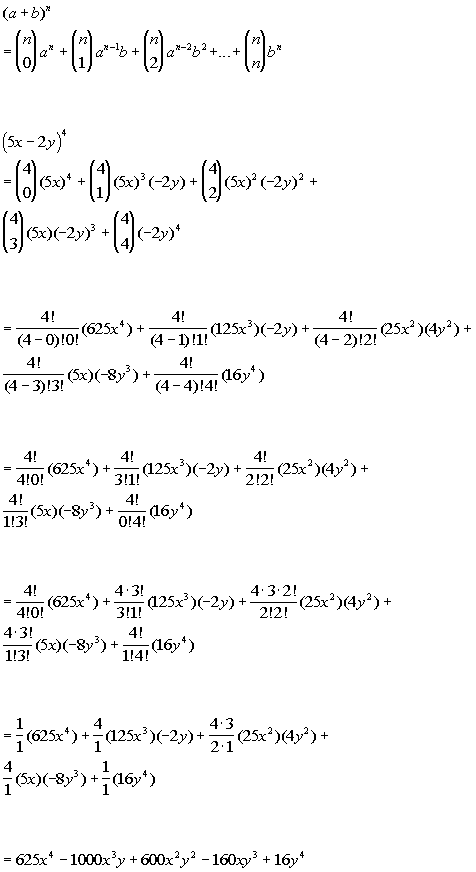
Wtamu Math Tutorials And Help

Pascal S Triangle And The Binomial Theorem

Binomial Theorem

Taylor Series Expansion

What Is The Correct Formula Of Math A B 3 Math Quora

Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab

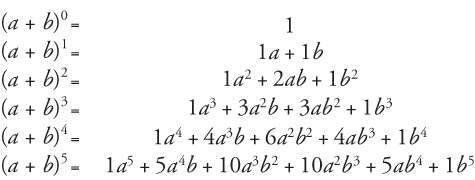
Binomial Coefficients And The Binomial Theorem

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

How To Expand Using The Identity A B C 2 B2 C2 2ab 2bc 2ca Youtube

What Is A B 3 Quora

A 2 B 2

Answer Plese All 4 Matching Pair Match The Following 3 Expand A 2 A Va Ctorize Xi 9x Math Expansion Formulae Meritnation Com

What Is The Formula Of Math A B 3 Math Quora

The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets

Misc 1 Find A B N In Expansion Of A B N If First Three

Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5

Derivation Of Formula For A B 3

Question Video Finding A Certain Term In A Binomial Expansion

Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange

Binomial Expansion Formula Examples Solutions Worksheets Videos Activities

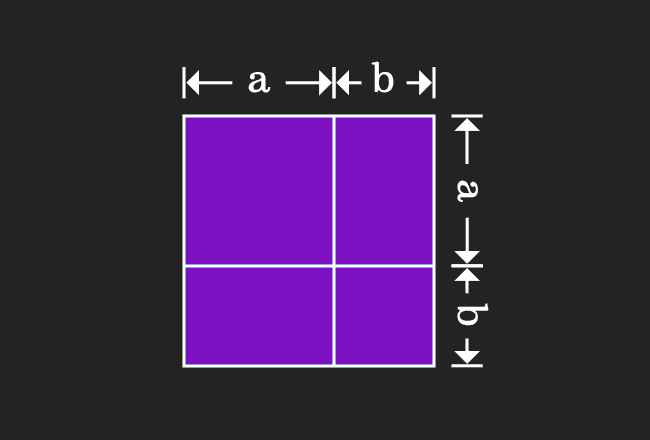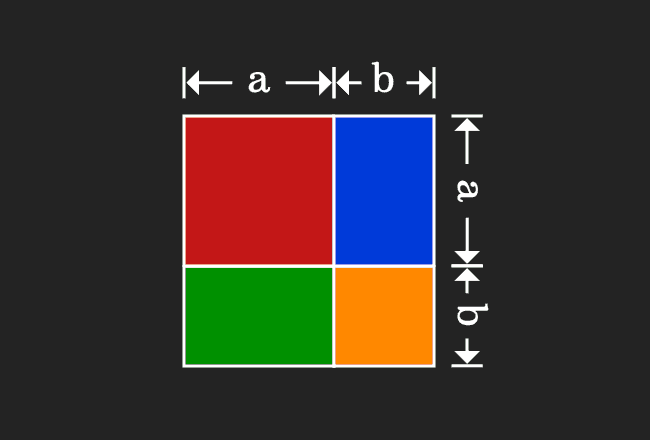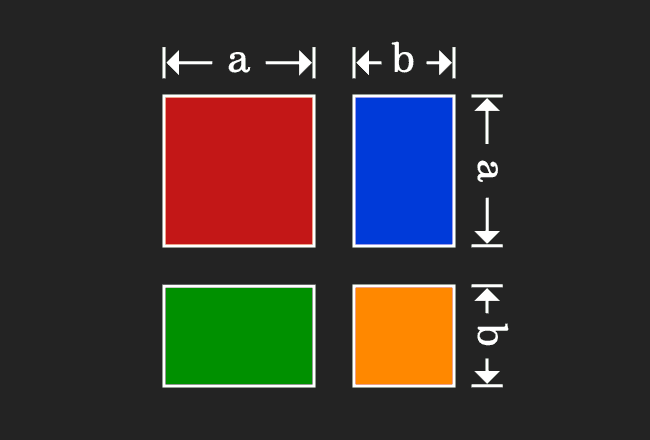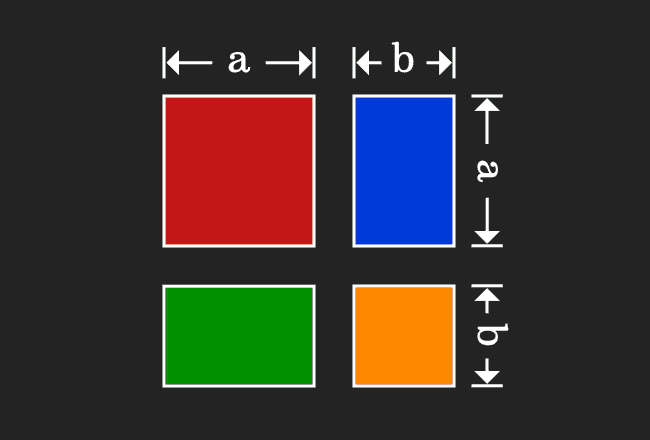
Proof Of A B Formula In Geometric Method

Expanding Algebraic Expressions Using Identities Worksheets

Pascal S Triangle

Solved It Is A Fact That The Taylor Series Expansion Aro Chegg Com

Standard Identities Of Binomials And Trinomials Equations Examples

Basic Expansion Of Algebraic Expressions For Children Math Methods Studying Math Algebraic Expressions

Wtamu Math Tutorials And Help

A Cube Plus B Cube Algebra Identity Derivation Youtube

Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning

Solved 3 10 Points A Find A Formula In Terms Of N Chegg Com

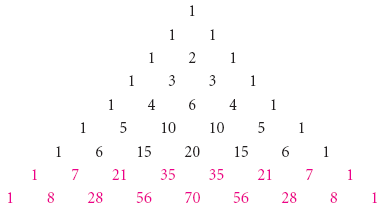
The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets

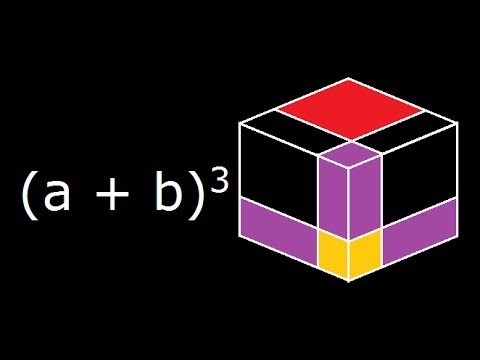
A B 3 A Plus B Cube Algebra Identity Geometrical Explanation And Derivation Youtube

Q Tbn And9gcrderb3nuifanmzhawkreaw0prjgnemsicomjvnkmiav92 A1kp Usqp Cau

A Cube Minus B Cube A 3 B 3 Geometrical Explanation And Derivation Of Algebra Identity Youtube

Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download

Incoming Term: (a+b)^3 formula expansion, (a+b+c)^3 formula expansion, what is a 3 b 3 formula, a+b expansion formula, how to expand a^3-b^3,